Complex Numbers: (lesson 2 of 2)
Polar representation
Polar representation of complex numbers
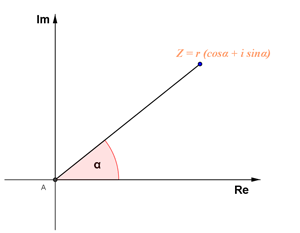
In polar representation a complex number z is represented by two parameters r and Θ . Parameter r is the modulus of complex number and parameter Θ is the angle with the positive direction of x-axis.
The polar form of a complex number is:
z = r ( cos θ + i sin θ ) z = r(\cos \theta + i\sin \theta ) z = r ( cos θ + i sin θ )
This representation is very useful when we multiply or divide complex numbers.
Polar to Rectangular Form Conversion
Here we know r and Θ and we need to find a and b .
Example 1:
Convert the complex number z = 4 ( cos 6 0 ∘ − i sin 6 0 ∘ ) z = 4(\cos {60^ \circ } - i\sin {60^ \circ }) z = 4 ( cos 6 0 ∘ − i sin 6 0 ∘ )
Solution:
z = 4 ( cos 6 0 ∘ − i sin 6 0 ∘ ) = 4 ( 1 2 − i 3 2 ) = 2 − 2 3 i z = 4(\cos {60^ \circ } - i\sin {60^ \circ }) = 4\left( {\frac{1}{2} - i\frac{{\sqrt 3 }}{2}} \right) = 2 - 2\sqrt {3i} z = 4 ( cos 6 0 ∘ − i sin 6 0 ∘ ) = 4 ( 2 1 − i 2 3 ) = 2 − 2 3 i
Exercise 1: Convert to rectangular form:
Rectangular to Polar Form Conversion
Here we know a and b and we need to find r and Θ . In this case we need to
use formulas:
r = a 2 + b 2 r = \sqrt {{a^2} + {b^2}} r = a 2 + b 2 t g θ = b a tg\theta = \frac{b}{a} t g θ = a b
Example 2:
Convert the complex number z = 2 − 2 3 i z = 2 - 2\sqrt {3i} z = 2 − 2 3 i
Solution:
In this example a = 2 a = 2 a = 2 b = − 2 3 b = - 2\sqrt 3 b = − 2 3
r = a 2 + b 2 = 2 2 + ( − 2 3 ) 2 = 4 + 12 = 4 r = \sqrt {{a^2} + {b^2}} = \sqrt {{2^2} + {{( - 2\sqrt 3 )}^2}} = \sqrt {4 + 12} = 4 r = a 2 + b 2 = 2 2 + ( − 2 3 ) 2 = 4 + 12 = 4 t g θ = b a = − 2 3 2 = − 3 ⇒ θ = − 6 0 ∘ tg\theta = \frac{b}{a} = \frac{{ - 2\sqrt 3 }}{2} = - \sqrt 3 \Rightarrow \theta = - {60^ \circ } t g θ = a b = 2 − 2 3 = − 3 ⇒ θ = − 6 0 ∘
The polar form is:
z = 4 ( cos ( − 6 0 ∘ ) + i sin ( − 6 0 ∘ ) ) = 4 ( cos 6 0 ∘ − i sin 6 0 ∘ ) z = 4(\cos ( - {60^ \circ }) + i\sin ( - {60^ \circ })) = 4(\cos {60^ \circ } - i\sin {60^ \circ }) z = 4 ( cos ( − 6 0 ∘ ) + i sin ( − 6 0 ∘ )) = 4 ( cos 6 0 ∘ − i sin 6 0 ∘ )
Exercise 2: Convert to polar form:
Product in polar representation
r ( cos θ − i sin θ ) ⋅ r ( cos θ t − i sin θ t ) = r ⋅ r t ( cos ( θ + θ t ) + i sin ( θ + θ t ) ) r(\cos \theta - i\sin \theta ) \cdot r(\cos {\theta ^t} - i\sin {\theta ^t}) = r \cdot {r^t}(\cos (\theta + {\theta ^t}) + i\sin (\theta + {\theta ^t})) r ( cos θ − i sin θ ) ⋅ r ( cos θ t − i sin θ t ) = r ⋅ r t ( cos ( θ + θ t ) + i sin ( θ + θ t ))
Example 3:
Let z 1 = 2 ( cos 3 0 ∘ + i sin 3 0 ∘ ) {z_1} = 2(\cos {30^ \circ } + i\sin {30^ \circ }) z 1 = 2 ( cos 3 0 ∘ + i sin 3 0 ∘ ) z 2 = 3 ( cos 12 0 ∘ + i sin 12 0 ∘ ) {z_2} = 3(\cos {120^ \circ } + i\sin {120^ \circ }) z 2 = 3 ( cos 12 0 ∘ + i sin 12 0 ∘ )
z 1 ⋅ z 2 = 2 ⋅ 3 ( cos ( 3 0 ∘ + 12 0 ∘ ) + i sin ( 3 0 ∘ + 12 0 ∘ ) ) = 6 ( cos 15 0 ∘ + i sin 15 0 ∘ ) {z_1} \cdot {z_2} = 2 \cdot 3(\cos ({30^ \circ } + {120^ \circ }) + i\sin ({30^ \circ } + {120^ \circ })) = 6(\cos {150^ \circ } + i\sin {150^ \circ }) z 1 ⋅ z 2 = 2 ⋅ 3 ( cos ( 3 0 ∘ + 12 0 ∘ ) + i sin ( 3 0 ∘ + 12 0 ∘ )) = 6 ( cos 15 0 ∘ + i sin 15 0 ∘ )
Quotient two complex numbers in polar representation
r ( cos τ + i sin τ ) r t ( cos θ + i sin θ ) = r r t ( cos ( τ − θ ) + i sin ( τ − θ ) ) \frac{{r(\cos \tau + i\sin \tau )}}{{{r^t}(\cos \theta + i\sin \theta )}} = \frac{r}{{{r^t}}}(\cos (\tau - \theta ) + i\sin (\tau - \theta )) r t ( c o s θ + i s i n θ ) r ( c o s τ + i s i n τ ) = r t r ( cos ( τ − θ ) + i sin ( τ − θ ))
Example 4:
Let z 1 = 2 ( cos 3 0 ∘ + i sin 3 0 ∘ ) {z_1} = 2(\cos {30^ \circ } + i\sin {30^ \circ }) z 1 = 2 ( cos 3 0 ∘ + i sin 3 0 ∘ ) z 2 = 3 ( cos 12 0 ∘ + i sin 12 0 ∘ ) {z_2} = 3(\cos {120^ \circ } + i\sin {120^ \circ }) z 2 = 3 ( cos 12 0 ∘ + i sin 12 0 ∘ )
z 1 z 2 = 2 3 ( cos ( 3 0 ∘ − 12 0 ∘ ) + i sin ( 3 0 ∘ − 12 0 ∘ ) ) = \frac{{{z_1}}}{{{z_2}}} = \frac{2}{3}(\cos ({30^ \circ } - {120^ \circ }) + i\sin ({30^ \circ } - {120^ \circ })) = z 2 z 1 = 3 2 ( cos ( 3 0 ∘ − 12 0 ∘ ) + i sin ( 3 0 ∘ − 12 0 ∘ )) = = 2 3 ( cos ( − 9 0 ∘ ) + i sin ( − 9 0 ∘ ) ) = = \frac{2}{3}(\cos ( - {90^ \circ }) + i\sin ( - {90^ \circ })) = = 3 2 ( cos ( − 9 0 ∘ ) + i sin ( − 9 0 ∘ )) = = 2 3 ( cos 9 0 ∘ − i sin 9 0 ∘ ) = \frac{2}{3}(\cos {90^ \circ } - i\sin {90^ \circ }) = 3 2 ( cos 9 0 ∘ − i sin 9 0 ∘ )
Exercise 3: Find product and quotient:
The inverse of a complex number in polar representation
1 r ( cos θ + i sin θ ) = 1 r ( cos θ − i sin θ ) \frac{1}{{r(\cos \theta + i\sin \theta )}} = \frac{1}{r}(\cos \theta - i\sin \theta ) r ( c o s θ + i s i n θ ) 1 = r 1 ( cos θ − i sin θ )
Conjugate numbers in polar representation
r ( cos θ + i sin θ ) ‾ = r ( cos θ − i sin θ ) \overline {r(\cos \theta + i\sin \theta )} = r(\cos \theta - i\sin \theta ) r ( cos θ + i sin θ ) = r ( cos θ − i sin θ )
Formula 'De Moivre'
( cos θ + i sin θ ) n = cos ( n θ ) + i sin ( n θ ) {(\cos \theta + i\sin \theta )^n} = \cos (n\theta ) + i\sin (n\theta ) ( cos θ + i sin θ ) n = cos ( n θ ) + i sin ( n θ )
Example 5:
Let z = 1 - i.
a) find polar representation
b) find z8
Solution:
a) z = 2 ( cos 4 5 ∘ + i sin 4 5 ∘ ) z = \sqrt 2 (\cos {45^ \circ } + i\sin {45^ \circ }) z = 2 ( cos 4 5 ∘ + i sin 4 5 ∘ )
b) z 8 = [ 2 ( cos 45 ∘ + i sin 45 ∘ ) ] 8 = 2 8 ⋅ ( cos 4 5 ∘ + i sin 4 5 ∘ ) 8 = 2 4 ⋅ ( cos ( 8 ⋅ 4 5 ∘ ) + i sin ( 8 ⋅ 4 5 ∘ ) ) = 16 ( cos 36 0 ∘ + i s i n 36 0 ∘ ) = 16 ( 1 + i ⋅ 0 ) = 16 {z^8} = {\left[ {\sqrt 2 (\cos {{45}^ \circ } + i\sin {{45}^ \circ })} \right]^8} = {\sqrt 2 ^8} \cdot {(\cos {45^ \circ } + i\sin {45^ \circ })^8} = {2^4} \cdot (\cos (8 \cdot {45^ \circ }) + i\sin (8 \cdot {45^ \circ })) = 16(\cos {360^ \circ } + isin{360^ \circ }) = 16(1 + i \cdot 0) = 16 z 8 = [ 2 ( cos 45 ∘ + i sin 45 ∘ ) ] 8 = 2 8 ⋅ ( cos 4 5 ∘ + i sin 4 5 ∘ ) 8 = 2 4 ⋅ ( cos ( 8 ⋅ 4 5 ∘ ) + i sin ( 8 ⋅ 4 5 ∘ )) = 16 ( cos 36 0 ∘ + i s in 36 0 ∘ ) = 16 ( 1 + i ⋅ 0 ) = 16
Exercise 4: Find zn :