- Math Lessons
- >
- Algebra
- >
- Rational Expressions
- >
- Multiplying and Dividing Rational Expressions
| « Simplifying Rational Expressions |
Multiplying and Dividing Rational Expressions
Multiplication
To Multiply a rational expression:
1. Factor all numerators and denominators.
2. Cancel all common factors.
3. Either multiply the denominators and numerators together or leave the solution in factored form.
Example 1
Multiply and then simplify the product
$\frac{{2x + 4}}{x} \cdot \frac{3}{{6x + 12}}$
Solution
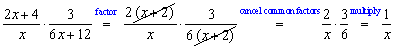
Example 2
Multiply the following rational expressions:
$\frac{{{x^2} + 6x + 9}}{{{x^2} - 9}} \cdot \frac{{3x - 9}}{{{x^2} + 2x - 3}}$
Solution
1: Factor all numerators and denominators:
$\frac{{{x^2} + 6x + 9}}{{{x^2} - 9}} \cdot \frac{{3x - 9}}{{{x^2} + 2x - 3}} = \frac{{(x + 3)(x + 3)}}{{(x - 3)(x + 3)}} \cdot \frac{{3(x - 3)}}{{(x + 3)(x - 1)}}$
2: Cancel all common factors:
$\frac{{{x^2} + 6x + 9}}{{{x^2} - 9}} \cdot \frac{{3x - 9}}{{{x^2} + 2x - 3}} = \frac{{\cancel{{(x + 3)}}\cancel{{(x + 3)}}}}{{\cancel{{(x - 3)}}\cancel{{(x + 3)}}}} \cdot \frac{{3\cancel{{(x - 3)}}}}{{\cancel{{(x + 3)}}(x - 1)}}$
3: Multiply the denominators and numerators:
$\frac{{{x^2} + 6x + 9}}{{{x^2} - 9}} \cdot \frac{{3x - 9}}{{{x^2} + 2x - 3}} = \frac{{\cancel{{(x + 3)}}\cancel{{(x + 3)}}}}{{\cancel{{(x - 3)}}\cancel{{(x + 3)}}}} \cdot \frac{{3\cancel{{(x - 3)}}}}{{\cancel{{(x + 3)}}(x - 1)}} = \frac{1}{1} \cdot \frac{3}{{x - 1}} = \frac{3}{{x - 1}}$
Division of rational expressions
When we divide rational functions we multiply by the reciprocal.
Example 3:
Perform the indicated operations:
$\frac{{2{x^2} + x - 6}}{{{x^2} - 2x - 8}}:\frac{{2{x^2} - x - 3}}{{{x^2} - 3x - 4}}$
Solution 3:
$$\frac{{2{x^2} + x - 6}}{{{x^2} - 2x - 8}}:\frac{{2{x^2} - x - 3}}{{{x^2} + 3x - 4}} = $$ $$ = \frac{{2{x^2} + x - 6}}{{{x^2} - 2x - 8}} \cdot \frac{{{x^2} - 3x - 4}}{{2{x^2} - x - 3}} = $$ $$ = \frac{{2\left( {x - \frac{3}{2}} \right)(x + 2)}}{{(x + 2)(x - 4)}} \cdot \frac{{(x - 4)(x + 1)}}{{2\left( {x - \frac{3}{2}} \right)(x + 1)}} = $$ $$ = \frac{{\bcancel{{(2x - 3)}}\cancel{{(x + 2)}}}}{{\cancel{{(x + 2)}}\bcancel{{(x - 4)}}}} \cdot \frac{{\bcancel{{(x - 4)}}\cancel{{(x + 1)}}}}{{\bcancel{{(2x - 3)}}\cancel{{(x + 1)}}}} = 1$$
Example 4:
Perform the indicated operations:
$\frac{{\frac{{x + 4}}{{2x - 6}}}}{{\frac{{3x + 12}}{{4x - 12}}}}$
Solution 4:
$$\frac{{\frac{{x + 4}}{{2x - 6}}}}{{\frac{{3x + 12}}{{4x - 12}}}} = \frac{{x + 4}}{{2x - 6}} \cdot \frac{{4x - 12}}{{3x + 12}} = $$ $$ = \frac{{\cancel{{x + 4}}}}{{2\cancel{{(x - 3)}}}} \cdot \frac{{4\cancel{{(x - 3)}}}}{{3\cancel{{(x + 4)}}}} = \frac{1}{2} \cdot \frac{4}{3} = \frac{2}{3}$$