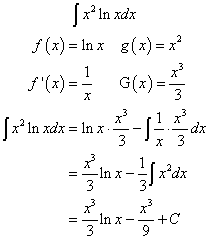- Math Lessons
- >
- Calculus
- >
- Integrals
- >
- Integration Formulas - Exercises
| « Integration Formulas |
|
Introduction to Integration: (lesson 2 of 2)
Integration Formulas - Exercises
1. Integration of polynomial functions
Formula 1.
$$ \color{blue}{ \int x^r dx = \frac{x^{r+1}}{r+1}+C} $$Exercise 1.
$$ \int x^{\color{red}{7}} dx = \frac{ x^{\color{red}{7}+1} }{\color{red}{7}+1} + C = \frac{x^8}{8}+C $$Formula 2.
$$ \color{blue}{ \int k \, dx = k\,x + C } ~ \text{ where } ~ k ~ \text{ is constant.} $$Exercise 2.
$$ \int \color{blue}{5} dx = \color{blue}{5}\,x + C $$Formula 3.
$$ \color{blue}{ \int k \cdot f(x) dx = k \int f(x) dx + C } ~ \text{ where } ~ k ~ \text{ is constant.} $$Exercise 3.
$$ \int \color{blue}{4} x^6 dx = \color{blue}{4} \int x^6 dx = 4 \cdot \frac{x^{6+1}}{6+1} + C = \frac{4}{7} x^7 + C$$Formula 4.
$$ \color{blue}{ \int f(x) \pm g(x) dx = \int f(x) dx \pm \int g(x) dx} $$Exercise 4.
$$ \begin{aligned} \int \color{red}{2x^2} + \color{blue}{3x} + 2 dx &= \int \color{red}{2x^2} dx + \int \color{blue}{3x} dx + \int 2 dx = \\\\ &= 2 \color{red}{\frac{x^{2+1}}{2+1}} + 3 \color{blue}{\frac{x^{1+1}}{1+1}} + 2x + C = \\\\ &= \frac{2}{3} x^3 + \frac{3}{2} x^2 + 2x + C \end{aligned} $$2. Integration of exponential and logarithmic functions
Formula 5.
$$ \color{blue}{ \int e^x dx = e^x + C} $$Exercise 5.
$$ \int 6 e^x dx = 6 \int e^x dx = 6 e^x + C $$Formula 6.
$$ \color{blue}{ \int e^{f(x)} \cdot f'(x) dx = e^{f(x)} + C} $$Exercise 6.
$$ \begin{aligned} \int e^{2x^2+1}\cdot \color{blue}{4x} dx &= \int e^{2x^2+1}\cdot \color{blue}{\left(2x^2+1\right)'} dx = \\\\ &= e^{2x^2+1}+C \end{aligned} $$Formula 7.
$$ \color{blue}{ \int \frac{1}{x} dx = \ln|x| + C} $$Exercise 7.
$$ \int \frac{5}{x} dx = 5 \int \frac{1}{x} dx = 5\,\ln|x| + C $$Formula 8.
$$ \color{blue}{ \int \frac{f'(x)}{f(x)} = \ln\,|f(x)| + C } $$Exercise 8a.
$$ \int \frac{\color{blue}{2x}}{x^2-1} dx = \int \frac{\color{blue}{(x^2-1)'}}{x^2-1} = \ln|x^2-1| + C $$Exercise 8b.
$$ \begin{aligned} \int \frac{x^2+1}{x^3+3x+2} dx &= \int \frac{\color{blue}{\frac{1}{3}(3x^2 + 3)}}{x^3+3x+2} dx = \\\\ &= \frac{1}{3} \int \frac{\color{blue}{(x^3+3x+2)'}}{x^3+3x+2} dx = \\\\ &= \frac{1}{3} \ln|x^3+3x+2| + C \end{aligned} $$3. Integration of trigonometric functions
Formula 9.
$$ \color{blue}{ \int \cos x \, dx = \sin x + C} $$Exercise 9.
$$ \int 3 \cos x \, dx = 3 \int \cos x \, dx = 3 \sin x + C $$Formula 10.
$$ \color{blue}{ \int \cos f(x) \cdot f'(x) dx = \sin f(x) + C} $$Exercise 10.
$$ \begin{aligned} \int x^2 \cos(x^3) dx &= \frac{1}{3} \int \color{blue}{3x^2} \cos(x^3) dx = \\\\ &= \frac{1}{3} \int \color{blue}{\left( x^3 \right)'} \cos(x^3) dx = \\\\ &= \frac{1}{3} \sin(x^3) + C \end{aligned} $$Formula 11.
$$ \color{blue}{ \int \sin x \, dx = - \cos x + C} $$Exercise 11.
$$ \int -2 \sin x \, dx = -2 \int \sin x \, dx = -2(- \cos x) + C = 2\cos x + C $$Formula 12.
$$ \color{blue}{ \int \sin f(x) \cdot f'(x) dx = - \cos f(x) + C } $$Exercise 12.
$$ \begin{aligned} \int x \sin \left(1+x^2\right) dx &= \frac{1}{2} \int \color{blue}{2x} \sin \left(1+x^2\right) dx = \\\\ &= \frac{1}{2} \int \color{blue}{\left(1+x^2\right)'} \sin \left(1+x^2\right) dx = \\\\ &= - \frac{1}{2} \cos \left( 1+x^2 \right) + C \end{aligned} $$Formula 13.
$$ \color{blue}{ \int \sec^2 x dx = \tan x + C} $$Exercise 13.
$$ \int 9 \sec^2 x dx = 9 \int \sec^2 x dx = 9 \tan x + C $$Formula 14.
$$ \color{blue}{ \int \sec^2 f(x) \cdot f'(x) dx = \tan f(x) + C } $$Exercise 14.
$$ \begin{aligned} \int x^3 \cdot \sec^2 \left(1+x^4\right) &= \frac{1}{4} \int \color{blue}{4x^3} \sec^2 \left(1+x^4\right) dx = \\\\ &= \frac{1}{4} \int \color{blue}{\left(1+x^4\right)'} \sec^2 \left(1+x^4\right) dx = \\\\ &= \frac{1}{4} \tan \left(1+x^4\right) + C \end{aligned} $$4. Integration by substitution
Formula 15.
$$ \color{blue}{ \int f(u) du = F(u) + C} ~ \text{where} ~ u=g(x) ~ \text{and} ~ du=g'(x)dx $$Also written as:
$$ \int f(g(x)) \cdot g'(x) dx = F(g(x)) + C $$Exercise 15a:
$$ \int 2x \cdot \left( x^2+4\right)^4 dx $$ $$ \begin{aligned} \color{red}{u} & \color{red}{=x^2 + 4} \\\\ \color{blue}{du}& \color{blue}{= 2x dx} \end{aligned} $$ $$ \begin{aligned} \int \color{blue}{2x} \cdot \color{red}{\left( x^2+4\right)^4} \color{blue}{dx} &= \int \color{red}{u^4} \color{blue}{du}= \\\\ &= \frac{u^5}{5} + C = \\\\ &= \frac{\left(x^2+4\right)^2}{5} + C \end{aligned} $$Exercise 15b:
$$ \int x^2 \cdot \sqrt{x^3+1} dx $$ $$ \begin{aligned} \color{red}{u} & \color{red}{=x^3 + 1} \\\\ \color{blue}{du}& \color{blue}{= 3x^2 dx} \end{aligned} $$
$$
\begin{aligned}
\int x^2 \sqrt{x^3+1} dx &= \frac{1}{3} \int \sqrt{\color{red}{x^3+1}} \, \color{blue}{3x^2 dx} = \\\\
&= \frac{1}{3} \int \sqrt{\color{red}{u}} \, \color{blue}{\, du} = \\\\
&= \frac{1}{3} \int u^{1 \backslash 2} \, du \\\\
&= \frac{1}{3} \frac{ u^{3 \backslash 2 }}{\frac{3}{2}} + C \\\\
&= \frac{2}{9} u^{3 \backslash 2}+C \\\\
&= \frac{2}{9} (x^3+1)^{3 \backslash 2}+C \\\\
&= \frac{2}{9} \sqrt{\left(x^3+1\right)^3} + C
\end{aligned}
$$
5. Integration by parts
Formula 16.
$$ \color{blue}{ \int f(x)g'(x) dx = f(x)g(x) - \int f'(x)g(x) dx } $$Also written as:
$$ \int u dv = uv - \int v du $$where
$$ \begin{aligned} u &= f(x) ~~,~~ dv = g(x)dx \\\\ du &=f'(x) ~~,~~ v = \int g(x) dx \end{aligned} $$Exercise 16: