Complex number calculator
This calculator performs all operations on complex numbers; it also finds the square root, modulus, inverse, conjugate and converts complex numbers to polar form. The solver explains each operation in detail, step by step.
Tutorial
What is complex number?
Each complex number has real and imaginary part. Complex number can be represented as z = a + bi. The i is a imaginary unit, which square is -1.
i2 = -1
This calculator performs five operations related to a single complex number: modulus, conjugate, inverse, roots and polar form, as well as four arithmetic operations. We will demonstrate how to solve each of these problems using five examples.
1 : Modulus - magnitude
The modulus or magnitude of a complex number (denoted by |z|) is the distance between the origin and that number.
If z = a + bi is a complex number, then the modulus is
$$ \color{blue}{|z| = \sqrt{a^2 + b^2}} $$
Example 1:
Find the modulus of z = 6 + 3i.
In this example, a = 6 and b = 3, so the modulus is:
$$ \begin{aligned} | z | &= \sqrt{ a^2 + b^2} = \sqrt{6^2 + 3^2} = \\[1 em] &= \sqrt{36 + 9} = \sqrt{45} = \\[1 em] &= \sqrt{9 \cdot 5} = 3 \sqrt{5} \end{aligned} $$The following video shows how to find modulus, polar form and conjugate.
2 : Conjugate
To find the complex conjugate of a complex number, we just need to change the sign of the imaginary part.
The conjugate of z = a + bi, is z=a – bi
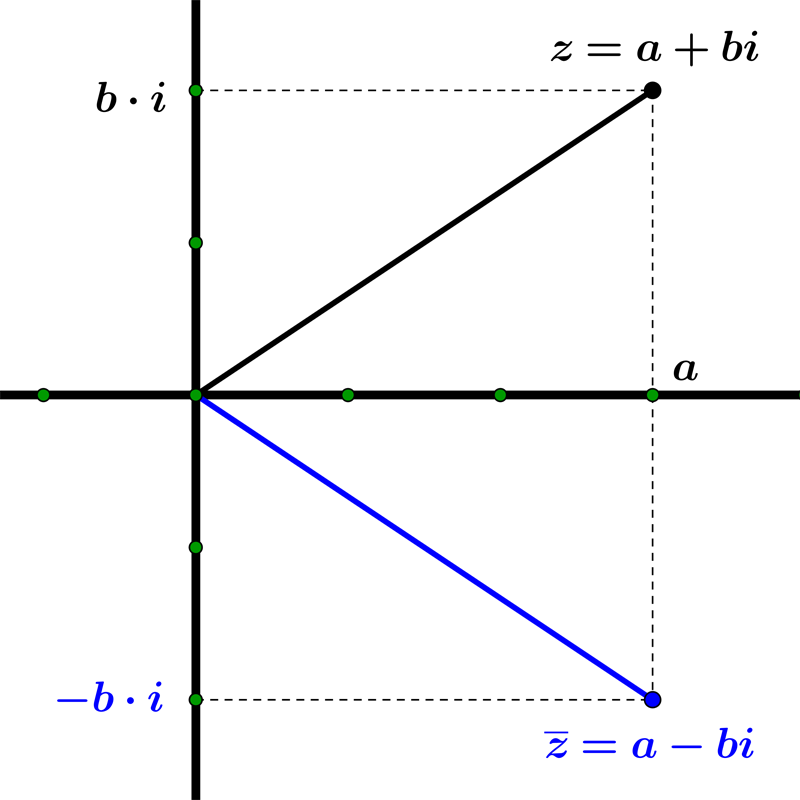
Example 02: The complex conjugate of z=3+4i is z=3-4i.
Example 03: The conjugate of z=-4i is z=4i.
Example 04: The conjugate of z=15 is z=15, too.
4 : Inverse
The inverse or reciprocal of a + bi is
$$ \color{blue}{ \frac{1}{a + b\,i}} $$Here is an example of how to find the inverse.
Example 06: Find the inverse of the number z=4+3i.
$$ \begin{aligned} \frac{1}{z} &= \frac{1}{4+3i} = \frac{1}{4+3i} \cdot \frac{4-3i}{4-3i} = \\[1 em] &= \frac{4-3i}{(4+3i)(4-3i)} = \frac{4-3i}{4^2 - (3i)^2} = \\[1 em] &= \frac{4-3i}{16+9} = \frac{4-3i}{25} = \frac{4}{25} - \frac{3}{25} i \end{aligned} $$5 : Polar Form
The polar form of a complex number z = a + ib is given as:
z = |z| ( cos α + i sin α)
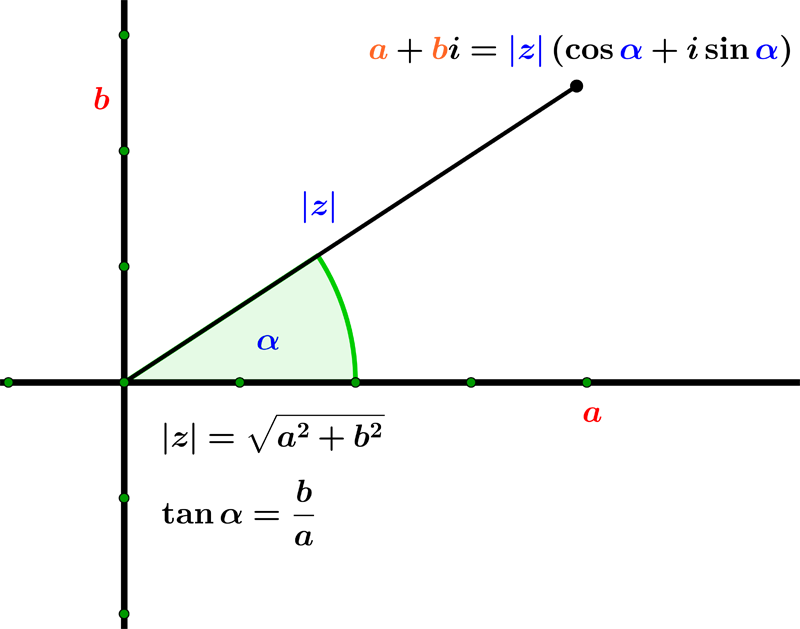
Example 05: Express the complex number z = 2 + i in polar form.
To find a polar form, we need to calculate |z| and α using formulas in the above image.
$$ |z| = \sqrt{2^2 + 1^2} = \sqrt{5}$$ $$ \tan \alpha = \dfrac{b}{a} = \dfrac{1}{2} \implies \alpha = \tan^{-1}\left(\dfrac{1}{2}\right) \approx 27^{o} $$So, the polar form is z = √5 (cos 27o + i sin 27o)