« Trigonometric Equations

The law of cosines is used:

1. to find the third side of a triangle when two sides and the included angle are given.

2. to find an angle when all 3 sides are given.

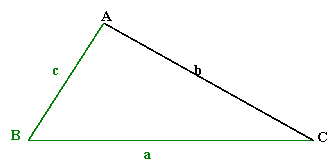
1. We are given $a$, $c$, and $\sphericalangle B$.

$$ \begin{aligned} b^2 &= a^2 + c^2 - 2ac\cos(\sphericalangle B) \\ b &= \sqrt{a^2 + c^2 - 2ac\cos(\sphericalangle B)} \end{aligned} $$

2. We are given sides $b$, $c$, and $\sphericalangle A$.

$$a = \sqrt{b^2 + c^2 - 2bc\cos(\sphericalangle A)}$$

3. We are given sides $b$, $a$, and $\sphericalangle C$.

$$c = \sqrt{a^2 + b^2 - 2ab\cos(\sphericalangle C)}$$

Example 1:

In triangle $ABC$, side $a= 8 cm$, $c = 10 cm$, and the angle at $B = 60^\circ$. Find side $b$, angle $A$ and angle $C$.

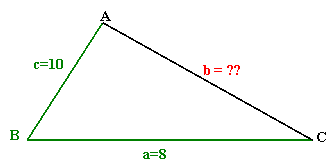
Solution:

1. Side $b$:

$$ \begin{aligned} b^2 &= a^2 + c^2 - 2ac\cos(\sphericalangle B) \\ b &= \sqrt{a^2 + c^2 - 2ac\cos(\sphericalangle B)} \\ b &= \sqrt{8^2 + 10^2 - 2 \cdot 8 \cdot 10 \cdot \cos(\sphericalangle 60^\circ)} \\ b &= \sqrt{164-80} \\ \color{blue}{b} &\color{blue}{=} \color{blue}{\sqrt{84} = 2 \sqrt{21}} \end{aligned} $$

2. Angle $A$

$$ \begin{aligned} a^2 &= b^2 + c^2 - 2bc\cos(\sphericalangle A) \\ 8^2 &= 10^2 + {\sqrt{84}}^2 - 2 \cdot 10 \cdot \sqrt{84} \cos(\sphericalangle A) \\ 64 &= 184 - 20 \sqrt{84} \cos(\sphericalangle A) \\ \cos(\sphericalangle A) &= \frac{120}{20 \sqrt{84}} \\ \cos(\sphericalangle A) &= \frac{6}{2\sqrt{21}} = \frac{3}{\sqrt{21}} \\ \color{blue}{\cos(\sphericalangle A)} &\color{blue}{=} \color{blue}{\arccos (\frac{3}{\sqrt{21}}) \approx 49.1^\circ} \end{aligned} $$

3. Angle $C$

$$ \begin{aligned} &\sphericalangle A + \sphericalangle B + \sphericalangle C = 180^\circ \\ &\arccos(\frac{3}{\sqrt{21}}) + 60^\circ + \sphericalangle C = 180^\circ \\ &\sphericalangle C = 120^\circ - \arccos (\frac{3}{\\sqrt{21}}) \approx 120^\circ - 49.1^\circ \\ &\sphericalangle C \approx 50.9^\circ \end{aligned} $$