« Area Between Two Curves

Arc Length »

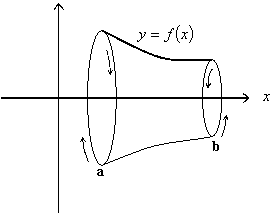
Definition 1

Let $f$ be continuous and nonnegative on $[a, b]$. Then, the volume of the solid generated by revolving the area below the graph of $f$ by x-axis between $x = a$ and $x = b \ \ (a < b)$ is defined by

$$V = \int\limits_a^b {\pi {{\left[ {f(x)} \right]}^2}dx}$$

Example 1:

Find the volume of the solid generated by revolving the region bounded by the graph of $f(x) = \sqrt{\sin x}$ and the axis $(0 \le x \le \pi)$ by the x-axis.

Solution:

$f(x) = \sqrt{\sin x}$ and the x-axis intersect at $(0, 0)$ and $(\pi, 0)$, so since

$$f(x) = 0 \leftrightarrow \sqrt{\sin x} = 0 \leftrightarrow x = 0, \pi, 2 \pi, . . .$$

Thus,

$$\begin{aligned} V &= \int\limits_a^b {\pi {{[f(x)]}^2}dx} = \pi \int\limits_0^z {{{(\sqrt {\sin x} )}^2}dx} = \pi \int\limits_0^z {\sin xdx} = \\ &= [ - \pi \cos x]_0^z = - \pi \cos (\pi ) + \pi \cos (0) = \\ &= 2 \pi \end{aligned}$$

Definition 2:

If the area is revolved about the y-axis, then the volume of the generated solid is defined by

$$V = \int\limits_a^b {2\pi xf(x)dx}$$

Example 2:

Find the volume of the solid generated by revolving the area below the graph of $f(x) = x - x^3$ and the x-axis about the y-axis.

Solution:

$f(x) = x - x^3$ and the x-axis intersect at $(0, 0)$ and $(2, 0)$ since

$f(x) = 0 \leftrightarrow x - x^3 = 0 \leftrightarrow x = 0,1$.

Then

$$\begin{aligned} V &= \int\limits_a^b {2\pi xf(x)dx = 2\pi \int\limits_0^1 {x(x - {x^3})dx = } } 2\pi \int\limits_0^1 {( - {x^4} + {x^2})dx = } \\ &= 2\pi \left[ {\frac{ - x^5}{5} + \frac{x^3}{5}} \right]_0^1 = \\ &= \frac{4 \pi}{15} \end{aligned}$$

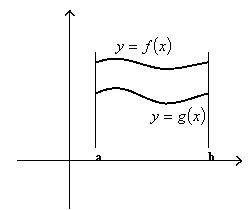
Volume by rotating the area between two curves

Let $f(x) \ge g(x)$. The volume generated by rotating the region bounded by the curves and lines $y = f(x)$, $y = g(x)$, $x = a$ and $x = b$ around the x-axis is defined by

$$V = \int\limits_a^b {\pi \left\{ {{{\left[ {f(x)} \right]}^2} - {{\left[ {g(x)} \right]}^2}} \right\}} dx$$

Example 3:

Find the volume of the solid generated by revolving the area bounded by the graphs of $f(x) = x^2$ and $g(x) = \sqrt{x}$ about the x-axis.

Solution:

The two lines intersect at the points $(0, 0$ and $(1,1)$ since

$$f(x) = g(x) \leftrightarrow x^2 = \sqrt{x} \leftrightarrow x^4 - x^2 = 0 \leftrightarrow x = -1, 0, 1.$$

Thus,

$$\begin{aligned} V &= \int\limits_a^b {\pi \left\{ {{{\left[ {f(x)} \right]}^2} - {{\left[ {g(x)} \right]}^2}} \right\}} dx = \pi \int\limits_0^1 {\left[ {{{(\sqrt x )}^2} - {{({x^2})}^2}} \right]dx} = \\ &= \pi \int\limits_0^1 {(x - {x^4})dx} = \pi \left[ {\frac{{{x^2}}}{2} - \frac{{{x^ \to }}}{5}} \right]_0^1 = \\ &= \frac{3\pi }{10} \end{aligned}$$