« Introduction to Determinant

Cramer's rule:

For linear system $A_{n \times n} x = b$, if $\det(A) \ne 0$, then the system has the unique solution,

$x_1 = \frac{\det(A_1)}{\det(A)}, x_2 = \frac{\det(A_2)}{\det(A)}, ..., x_n = \frac{\det(A_n)}{\det(A)}$

where $A_i, \ \ i = 1,2,...,n$, is the matrix obtained by replacing the i-th column of $A$ by $b$.

Example 1:

Solve the following system of linear equations using the Cramer's rule,

$\begin{aligned} &x_1 + 3x_2 + x_3 = -2 \\ &2x_1 + 5x_2 + x_3 = -5 \\ &x_1 + 2x_2 + 3x_3 = 6 \end{aligned}$

Solution:

The coefficient matrix A and the vector b are

A = \left[ {} \right], b = \left[ {} \right]

respectively. Then,

A = \left[ {} \right], {A_2} = \left[ {} \right], {A_3} = \left[ {} \right]

Thus, $x_1 = \frac{\det(A_1)}{\det(A)} = \frac{-3}{-3} = 1 , \ x_2 = \frac{\det(A_2)}{\det(A)} = \frac{6}{-3} = -2 , \ x_3 = \frac{\det(A_3)}{\det(A)} = 3$.

Areas:

Triangle:

Consider the triangle with vertices $(x_1, y_1)$, $(x_2, y_2)$ and $(x_3, y_3)$.

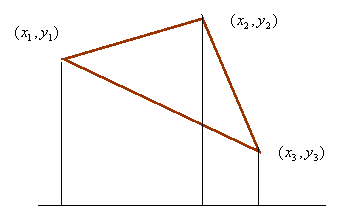
The area of the triangle is

\frac{1}{2}\left| {\left| {} \right|} \right| = \frac{1}{2}\left| {\det \left( {\left[ {} \right]} \right)} \right|.

Example 2:

Calculate the area of the triangle with vertices $(-1, 4)$, $(3,1)$ and $(2, 6)$.

Solution:

The area is

\frac{1}{2}\left| {\det \left( {\left[ {} \right]} \right)} \right| = \frac{1}{2} \cdot \left| {17} \right| = \frac{1}{2} \cdot 17 = 8.5 .

Parallelogram:

Suppose we have a parallelogram with vertices $(x_1, y_1)$, $(x_2, y_2)$, $(x_3, y_3)$ and $(x_4, y_4)$,

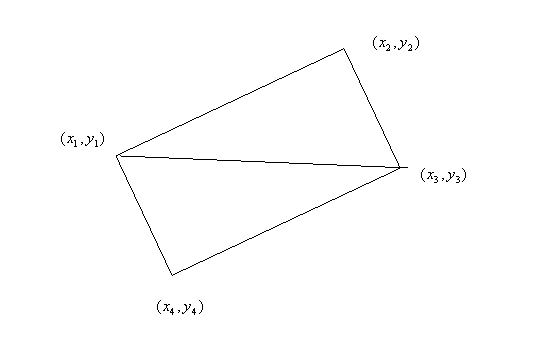
Then, the area of the parallelogram is

2 \cdot \frac{1}{2} \cdot \left| {\det \left( {\left[ {} \right]} \right)} \right| = \left| {\det \left( {\left[ {} \right]} \right)} \right|