- Math Formulas
- ::
- Functions
- ::
- Trigonometry formulas
Math formulas: Trigonometry identities
| 0 formulas included in custom cheat sheet | ||
Right-Triangle Definitions
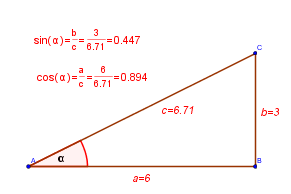
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Reduction Formulas

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Basic Identities
|
|
|
|
|
|
|
|
|
Sum and Difference Formulas
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Double Angle and Half Angle Formulas
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Other Useful Trig Formulas
Law of sines
|
|
|
Law of cosines
|
|
|
Area of triangle
|
|
|
Please tell me how can I make this better.