Triangle calculator

This calculator computes all the main triangle parameters, such as area, medians, altitudes, centroid and incenter. The calculator shows a formula and an explanation for each parameter of a triangle.

Triangle in coordinate geometry

Input vertices and choose one of seven triangle characteristics to compute.
help ↓↓ examples ↓↓ tutorial ↓↓

0123456789–/√.C ✖

First point A =

( , )

Second point B =

( , )

Third point C =

( , )

Find:

Area	Medians	Altitudes
Centroid (intersection of medians)
Incenter (center of the incircle)
Circumcenter (center of circumscribed circle)
Orthocenter (intersection of the altitudes)

Settings:

Hide steps

Find approximate solution

thumb_up 714 thumb_down

Get Widget Code

working...

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Examples

ex 1:

Find area of a triangle whose vertices are

(4, 4), (- 2, 3)

and

(- 4, - 5)

ex 2:

Find area of a triangle whose vertices are

(\frac{4}{3}, 3.5), (8, - \frac{1}{2})

and

(- 7, 5.2)

ex 3:

Find altitudes of a triangle whose vertices are

(1, 1), (3, 5)

and

(- 10, 8)

ex 4:

Find circumcenter of a triangle whose vertices are

(- 2, - 5), (3, 4)

and

(10, - 3)

Related calculators

Distance

Right triangle calculator

Equilateral triangle calculator

Sine cosine law

Find more worked-out examples in our database of solved problems.

Formulas and examples for triangle

Area of the triangle?

The area of a triangle whose vertices are $A (x_{A}, y_{A}), B (x_{B}, y_{B})$ and $C (x_{C}, y_{C})$ is given by :

K = \frac{1}{2} ∣ x_{A} (y_{B} - y_{C}) + x_{B} (y_{C} - y_{A}) + x_{C} (y_{A} - y_{B}) ∣

Example:

Find the area of the triangle whose vertices are $A (2, 4), B (3, - 1)$ and $C (- 3, 3)$ .

Solution:

In this example we have: $x_{A} = 2, y_{A} = 4, x_{B} = 3, y_{B} = - 1, x_{C} = - 3, y_{C} = 3$ . So we have:

K K K K K K K = \frac{1}{2} ∣ x_{A} (y_{B} - y_{C}) + x_{B} (y_{C} - y_{A}) + x_{C} (y_{A} - y_{B}) ∣ = \frac{1}{2} ∣2 (- 1 - 3) + 3 (3 - 4) - 3 (4 - (- 1)) ∣ = \frac{1}{2} ∣2 \cdot (- 4) + 3 \cdot (- 1) - 3 \cdot 5∣ = \frac{1}{2} ∣ - 8 - 3 - 15∣ = \frac{1}{2} ∣ - 26∣ = \frac{1}{2} \cdot 26 = 13

Centroid of the triangle?

The centroid of a triangle whose vertices are $A (x_{A}, y_{A}), B (x_{B}, y_{B})$ and $C (x_{C}, y_{C})$ is given by :

(x, y) = (\frac{x _{A} + x _{B} + x _{C}}{3}, \frac{y _{A} + y _{B} + y _{C}}{3})

Example:

Find the centroid of the triangle whose vertices are $A (2, 4), B (3, - 1)$ and $C (- 3, 3)$ .

Solution:

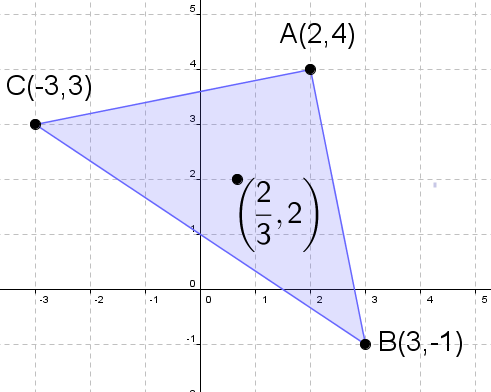
Using the same $x_{A}, y_{A}, x_{B}, y_{B}, x_{C}, y_{C}$ , as in previous example we have:

(x, y) (x, y) (x, y) = (\frac{x _{A} + x _{B} + x _{C}}{3}, \frac{y _{A} + y _{B} + y _{C}}{3}) = (\frac{2 + 3 - 3}{3}, \frac{4 - 1 + 3}{3}) = (\frac{2}{3}, 2)

Search our database with more than 300 calculators

452 861 664 solved problems