Two point form calculator

This online calculator finds and plots the equation of a straight line passing through the two given points. The calculator generates a step-by-step explanation of how to get the result.

Line through two points calculator

Find the line equation in both general and slop y-intercept form.
help ↓↓ examples ↓↓ tutorial ↓↓

0123456789–/.√C ✖

Input point A:

( , )

Input point B:

( , )

Display resulting line in:

General form (default)

Slope y-intercept form

Settings:

Hide steps

Find approximate solution

thumb_up 2K thumb_down

Get Widget Code

working...

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Examples

ex 1:

Determine the equation of a line passing through the points

(- 2, 5)

and

(4, - 2)

ex 2:

Find the slope - intercept form of a straight line passing through the points

(\frac{7}{2}, 4)

and

(\frac{1}{2}, 1)

ex 3:

If points

(3, - 5)

and

(- 5, - 1)

are lying on a straight line, determine the slope-intercept form of the line.

Related calculators

Graphing lines

Distance

Line - point distance

Lines intersection

Find more worked-out examples in our database of solved problems.

How to find equation of the line determined by two points?

To find equation of the line passing through points $A (x_{A}, y_{A})$ and $B (x_{B}, y_{B})$ ( $x_{A} \neq = x_{B}$ ), we use formula:

y - y_{A} = \frac{y _{B} - y _{A}}{x _{B} - x _{A}} (x - x_{A})

Example:

Find the equation of the line determined by $A (- 2, 4)$ and $B (3, - 2)$ .

Solution:

In this example we have: $x_{A} = - 2, y_{A} = 4, x_{B} = 3, y_{B} = - 2$ . So we have:

y - y_{A} y - 4 y - 4 = \frac{y _{B} - y _{A}}{x _{B} - x _{A}} (x - x_{A}) = \frac{- 2 - 4}{3 - ( - 2 )} (x - (- 2)) = \frac{- 6}{5} (x + 2)

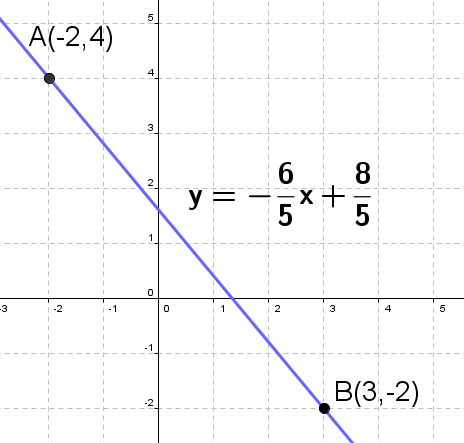
Multiply both sides with $5$ to get rid of the fractions.

(y - 4) \cdot 5 5 y - 20 5 y - 20 5 y 5 y y = \frac{- 6}{5} \cdot 5 (x + 2) = - 6 (x + 2) = - 6 x - 12 = - 6 x - 12 + 20 = - 6 x + 8 = - \frac{6}{5} x - \frac{8}{5}

In special case (when $x_{A} = x_{B}$ the equation of the line is:

x = x_{A}

Example 2:

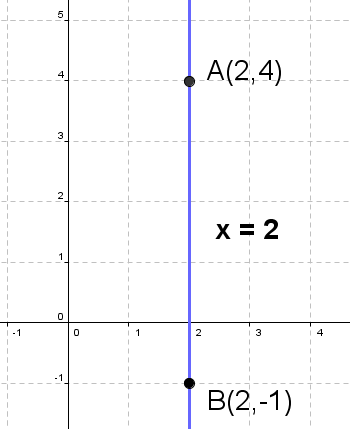
Find the equation of the line determined by $A (2, 4)$ and $B (2, - 1)$ .

Solution:

In this example we have: $x_{A} = 2, y_{A} = 4,$ $x_{B} = 2, y_{B} = - 1$ . Since $x_{A} = x_{B}$ , the equation of the line is:

x = 2

You can see from picture on the right that in special case the line is parallel to y - axis.

Note: use above calculator to check the results.

Search our database with more than 300 calculators

452 861 664 solved problems