About Graphing Quadratic Functions

Quadratic function has the form $f(x)=a{x}^2+bx+c$ where a, b and c are numbers

You can sketch quadratic function in 4 steps. I will explain these steps in following examples.

Example 1:

Sketch the graph of the quadratic function

$$f(x)=x^2+2x-3$$

Solution:

In this case we have $a=1,b=2$ and $c=-3$

STEP 1: Find the vertex.

To find x - coordinate of the vertex we use formula:

$$x=-\frac{b}{2a}$$

So, we substitute $1$ in for $a$ and $2$ in for $b$ to get

$$x=-\frac{b}{2a}=-\frac{2}{2\cdot 1}=-1$$

To find y - coordinate plug in $x=-1$ into the original equation:

$$y=f(-1)=(-1{)}^2+2\cdot (-1)-3=1-2-3=-4$$

So, the vertex of the parabola is $(-1,-4)$

STEP 2: Find the y-intercept.

To find y - intercept plug in $x=0$ into the original equation:

$$f(0)=(0{)}^2+2\cdot (0)-3=0-0-3=-3$$

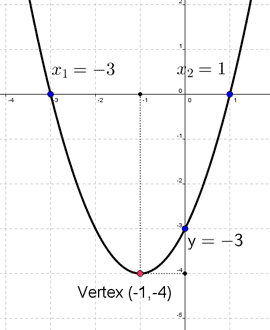
So, the y-intercept of the parabola is $y=-3$

STEP 3: Find the x-intercept.

To find x - intercept solve quadratic equation $f(x)=0$ in our case we have:

$$x^2+2x-3=0$$

Solutions for this equation are:

$$x_1=-3\text{and}{x}_2=1$$

( to learn how to solve quadratic equation use quadratic equation solver )

STEP 4: plot the parabola.

Example 2:

Sketch the graph of the quadratic function

$$f(x)=-x^2+2x-2$$

Solution:

Here we have $a=-1,b=2$ and $c=-2$

The x-coordinate of the vertex is:

$$x=-\frac{b}{2a}=-\frac{2}{2\cdot (-1)}=1$$

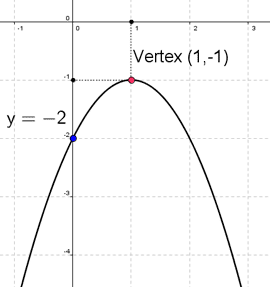
The y-coordinate of the vertex is:

$$y=f(1)=-1^2+2\cdot 1-2=-1+2-2=-1$$

The y-intercept is:

$$y=f(0)=-0^2+2\cdot 0-2=-0+0-2=-2$$

In this case x-intercept doesn't exist since equation $-x^2+2x-2=0$ does not has the solutions (use quadratic equation solver to check ). So, in this case we will plot the graph using only two points