Z - score calculator

This calculator solves three types of problems related to z-scores. 1. Find the area (probability) to the left, right, or between two Z-scores. 2. Find the z-score if the cumulative probability level (p-value) is given. 3. Find the z-score based on the raw value, mean and standard deviation of a population.

Tutorial

What is z – score?

The z-score measures how many standard deviations the observed value is above or below the population mean.

Z scores were created so that we could easily compare some data to the average value.

For example, knowing that someone is 175 cm tall doesn't tell us anything about how that person compares to the rest of the population. Is this person higher or smaller than average? On the other hand, if person's height has a z-score of 0.15, it means he is somewhat higher than the average; furthermore, we can calculate that he is taller than 55% of the population.

How to calculate z - score?

Case 1: If we know the raw score (x), mean (μ) and standard deviation (σ), we calculate the z-score using the following formula.

Z = (x - μ)/σ

Example: Given x = 72, μ = 65, and σ = 5, the z-score would be

Z = (x - μ)/σ = (72-65)/5 = 1.4

Thus, the number 72 is 1.4 standard deviations above the population mean.

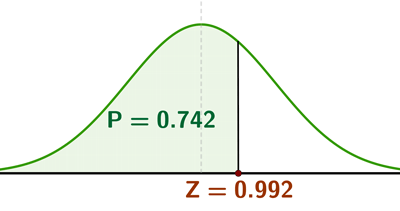
Case 2: If we know the p-value, we can calculate the z-score using the standard normal table.

For example if p = 0.742 than, using the standard normal table we can find that the z-score is 0.9920.

Case 3: If we are given a dataset, then we need to apply the following steps.

1. Calculate the mean μ using the formula μ = Σx/n,

2. Calculate the standard deviation using σ formula σ² = Σ(x - μ)² / (n-1),

3. Apply the formula Z = (x - μ)/σ.

Example: The dataset of exam scores is 45, 51, 67 and 55. Find the z-score for x = 60.

Step1: Find the mean.

μ = (45+61+67+55)/4 = 57

Step2: Find the standard deviation.

σ² = [(45-57)²+(61-57)²+(67-57)²+(55-57)²]/(4-1)
σ² = [(144+16+100+4]/3
σ² = 88
σ = 9.38

Step3: Calculate z

z = (60 - 57)/9.38 = 0.319

How to interpret z - score?

The z score shows how many standard deviations you are above or below the population mean.

Positive z-score indicates that the observation is above average.

Negative z-score indicates that the observation is below average.

Approximately 68% of the data have a z-score of -1 to 1. This means that 68% of observations are less than one standard deviation away from the mean. If your z score on the exam is 1.5, you are far above the average. On the other side, a z-score of -0.25 indicates that you are slightly below average.

Z-score table

The p-value is shown by the green number, and the z-score is presented by the orange numbers. Every value in the table represents the area between Z=0 and a Z-score.

z	0	0.01	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
0.0	0	0.0040	0.0080	0.0120	0.0159	0.0199	0.0239	0.0279	0.0318	0.0358
0.1	0.0398	0.0438	0.0479	0.0517	0.0557	0.0596	0.0635	0.0674	0.0714	0.0753
0.2	0.0793	0.0832	0.0871	0.0909	0.0948	0.0987	0.1025	0.1064	0.1102	0.1140
0.3	0.1179	0.1217	0.1255	0.1293	0.1331	0.1368	0.1405	0.1443	0.1480	0.1517
0.4	0.1554	0.1591	0.1628	0.1664	0.1700	0.1736	0.1772	0.1808	0.1843	0.1879
0.5	0.1915	0.1950	0.1985	0.2019	0.2054	0.2088	0.2122	0.2156	0.2190	0.2224
0.6	0.2257	0.2291	0.2324	0.2357	0.2389	0.2421	0.2453	0.2485	0.2517	0.2549
0.7	0.2580	0.2611	0.2642	0.2673	0.2704	0.2733	0.2763	0.2793	0.2823	0.2852
0.8	0.2881	0.2910	0.2939	0.2967	0.2995	0.3023	0.3051	0.3078	0.3105	0.3132
0.9	0.3159	0.3186	0.3212	0.3238	0.3264	0.3289	0.3314	0.3339	0.3364	0.3389
1.0	0.3413	0.3438	0.3461	0.3485	0.3508	0.3531	0.3554	0.3576	0.3599	0.3621
1.1	0.3643	0.3665	0.3686	0.3708	0.3729	0.3749	0.3769	0.3790	0.3810	0.3829
1.2	0.3849	0.3869	0.3888	0.3906	0.3925	0.3943	0.3961	0.3979	0.3997	0.4014
1.3	0.4032	0.4049	0.4066	0.4082	0.4099	0.4114	0.4130	0.4146	0.4162	0.4177
1.4	0.4192	0.4207	0.4222	0.4236	0.4251	0.4264	0.4278	0.4292	0.4305	0.4318
1.5	0.4332	0.4345	0.4358	0.4370	0.4382	0.4394	0.4406	0.4417	0.4429	0.4440
1.6	0.4452	0.4463	0.4474	0.4485	0.4495	0.4505	0.4515	0.4525	0.4535	0.4544
1.7	0.4554	0.4564	0.4573	0.4582	0.4591	0.4599	0.4608	0.4616	0.4624	0.4632
1.8	0.4641	0.4648	0.4656	0.4664	0.4671	0.4678	0.4685	0.4692	0.4699	0.4706
1.9	0.4713	0.4719	0.4726	0.4732	0.4738	0.4744	0.4750	0.4755	0.4761	0.4767
2.0	0.4772	0.4778	0.4783	0.4788	0.4793	0.4798	0.4803	0.4807	0.4812	0.4816
2.1	0.4821	0.4826	0.4830	0.4834	0.4838	0.4842	0.4846	0.4850	0.4853	0.4857
2.2	0.4861	0.4864	0.4868	0.4871	0.4875	0.4877	0.4880	0.4884	0.4887	0.4889
2.3	0.4893	0.4896	0.4898	0.4901	0.4904	0.4906	0.4908	0.4911	0.4913	0.4915
2.4	0.4918	0.4920	0.4922	0.4925	0.4927	0.4928	0.4930	0.4932	0.4934	0.4936
2.5	0.4938	0.4939	0.4941	0.4943	0.4945	0.4946	0.4947	0.4949	0.4950	0.4952
2.6	0.4953	0.4955	0.4956	0.4957	0.4958	0.4959	0.4960	0.4962	0.4963	0.4964
2.7	0.4965	0.4966	0.4967	0.4968	0.4969	0.4970	0.4971	0.4972	0.4972	0.4973
2.8	0.4974	0.4975	0.4976	0.4977	0.4977	0.4978	0.4978	0.4979	0.4980	0.4980
2.9	0.4981	0.4982	0.4983	0.4983	0.4983	0.4984	0.4984	0.4985	0.4985	0.4986
3.0	0.4986	0.4987	0.4987	0.4988	0.4988	0.4988	0.4988	0.4989	0.4989	0.4990