Calculators
::
2D Shapes
::
Right Triangle Calculator

Right triangle calculator

The right triangle calculator finds the missing area, angle, leg, hypotenuse and height of a triangle. The calculator also provides steps on how to solve the most important right triangles: the 30-60-90 triangle and the 45-45-90 triangle.

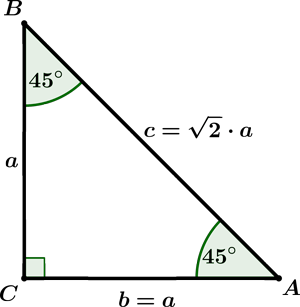Find two sides of a triangle ABC if hypotenuse c= $ \frac{ 41 }{ 5 }$ .

solution

Shorter leg $ a = \dfrac{ 41 }{ 10 } $

Long leg $ b = \dfrac{ 41 \sqrt{ 3}}{ 10 } $

explanation

Step 1: Find short leg a

From the diagram above we can see that $ c = 2 \cdot a $. In this example we have:

$$ \begin{aligned} c &= 2 \cdot a \\[1.3 em] \frac{ 41 }{ 5 } &= 2 \cdot a \\[1.3 em] a &= \dfrac{ \frac{ 41 }{ 5 } }{ 2} \\[1.3 em] a &= \frac{ 41 }{ 10 } \end{aligned} $$

ID	Problem	Count
1	Find the leg $ a $ of a right triangle if ???.	90
2	Find the angle $ \alpha $ of a right triangle if leg $a = 4$ and leg $b = 8$.	20
3	Find the leg $ b $ of a right triangle if hypotenuse $c = 2 \sqrt{ 17 }$ and angle $\alpha = 30^o$.	18
4	Find the angle $ \alpha $ of a right triangle if leg $a = 1$ and leg $b = 2$.	16
5	Find the leg $ a $ of a right triangle if leg $b = 8$ and hypotenuse $c = 17$.	15
6	Find the angle $ \alpha $ of a right triangle if leg $a = 8$ and hypotenuse $c = 14$.	14
7	Find the leg $ b $ of a right triangle if leg $a = 6$ and angle $\beta = 30^o$.	13
8	Find the hypotenuse $ c $ of a right triangle if leg $b = 8$ and angle $\alpha = 60^o$.	13
9	Find the hypotenuse $ c $ of a right triangle if leg $a = 51$ and leg $b = 140$.	13
10	Find the leg $ a $ of a right triangle if leg $a = 4$ and angle $\beta = 50^o$.	11
11	Find the leg $ b $ of a right triangle if leg $a = 4$ and angle $\beta = 50^o$.	10
12	Find the leg $ a $ of a right triangle if leg $b = 5$ and angle $\alpha = 30^o$.	10
13	Find the hypotenuse $ c $ of a right triangle if leg $b = 15$ and angle $\alpha = 60^o$.	10
14	Find the angle $ \beta $ of a right triangle if leg $a = 3$ and area $A = 90$.	10
15	Find the angle $ \beta $ of a right triangle if leg $b = 4$ and area $A = 90$.	10
16	Find the angle $ \beta $ of a right triangle if leg $a = 61$ and leg $b = 41$.	9
17	Find the angle $ \beta $ of a right triangle if leg $a = 2$ and leg $b = 1$.	9
18	Find the hypotenuse $ c $ of a right triangle if leg $a = 4$ and angle $\beta = 50^o$.	9
19	Find the hypotenuse $ c $ of a right triangle if leg $b = 39$ and angle $\beta = 60^o$.	9
20	Find the leg $ b $ of a right triangle if hypotenuse $c = \sqrt{ 6 }$ and angle $\beta = 45^o$.	9
21	Find the hypotenuse $ c $ of a right triangle if leg $a = 13$ and angle $\beta = 16^o$.	9
22	Find the leg $ b $ of a right triangle if leg $a = 7$ and hypotenuse $c = 16$.	9
23	Find the leg $ a $ of a right triangle if leg $b = 10$ and hypotenuse $c = 20$.	9
24	Find the angle $ \beta $ of a right triangle if leg $a = \frac{ 37 }{ 2 }$ and hypotenuse $c = \frac{ 229 }{ 10 }$.	9
25	Find the leg $ a $ of a right triangle if hypotenuse $c = 37$ and angle $\alpha = 15^o$.	9
26	Find the angle $ \beta $ of a right triangle if leg $a = \sqrt{ 39 }$ and leg $b = \sqrt{ 33 }$.	8
27	Find the leg $ a $ of a right triangle if leg $b = 75$ and angle $\alpha = 10^o$.	8
28	Find the angle $ \beta $ of a right triangle if leg $a = 7$ and hypotenuse $c = 16$.	8
29	Find the leg $ a $ of a right triangle if leg $b = 16$ and angle $\alpha = 37^o$.	8
30	Find the hypotenuse $ c $ of a right triangle if leg $a = 3$ and leg $b = 5$.	8
31	Find the leg $ b $ of a right triangle if hypotenuse $c = 20$ and angle $\beta = 74^o$.	8
32	Find the hypotenuse $ c $ of a right triangle if leg $a = 144$ and leg $b = 156$.	8
33	Find the leg $ b $ of a right triangle if leg $a = \frac{ 37 }{ 2 }$ and hypotenuse $c = \frac{ 229 }{ 10 }$.	8
34	Find the angle $ \beta $ of a right triangle if leg $a = \frac{ 957 }{ 100 }$, leg $b = \frac{ 1787 }{ 50 }$, hypotenuse $c = 37$ and angle $\alpha = 15^o$.	8
35	Find the leg $ a $ of a right triangle if hypotenuse $c = 10$, angle $\alpha = 45^o$ and angle $\beta = 45^o$.	7
36	Find the hypotenuse $ c $ of a right triangle if leg $a = 12$ and angle $\beta = 30^o$.	7
37	Find the leg $ a $ of a right triangle if hypotenuse $c = 7 \sqrt{ 2 }$ and angle $\beta = 45^o$.	7
38	Find the leg $ a $ of a right triangle if hypotenuse $c = 2$.	7
39	Find the angle $ \alpha $ of a right triangle if leg $a = 4$ and leg $b = 9$.	7
40	Find the leg $ b $ of a right triangle if leg $a = 13$ and angle $\alpha = 76^o$.	7
41	Find the hypotenuse $ c $ of a right triangle if leg $b = 4 \sqrt{ 3 }$ and angle $\beta = 60^o$.	7
42	Find the hypotenuse $ c $ of a right triangle if leg $a = 10$ and leg $b = 15$.	7
43	Find the leg $ b $ of a right triangle if leg $a = \frac{ 106 }{ 5 }$ and angle $\alpha = 71^o$.	7
44	Find the hypotenuse $ c $ of a right triangle if leg $a = 2$ and leg $b = 4$.	7
45	Find the leg $ a $ of a right triangle if leg $a = 12$ and hypotenuse $c = 15$.	7
46	Find the leg $ b $ of a right triangle if hypotenuse $c = 6$ and angle $\beta = 70^o$.	6
47	Find the hypotenuse $ c $ of a right triangle if leg $a = \frac{ 21 }{ 4 }$ and leg $b = \frac{ 99 }{ 8 }$.	6
48	Find the hypotenuse $ c $ of a right triangle if ???.	6
49	Find the hypotenuse $ c $ of a right triangle if leg $a = 2$ and leg $b = 2$.	6
50	Find the angle $ \beta $ of a right triangle if leg $a = 60$ and leg $b = 35$.	6

Right triangle calculator

Find two sides of a triangle ABC if hypotenuse c= $ \frac{ 41 }{ 5 }$ .

Report an Error!

Right Triangle – Solved Problems Database