- Calculators
- ::
- Numbers
- ::
- LCM Calculator
LCM calculator
LCM calculator computes Least common multiple of two or more numbers using five methods. (division method, listing multiples method, prime factors, ladder method and the LCM formula). The calculator shows a full step-by-step solution of each method, along with a Venn diagram.
Find Least Common Multiple of 60, 84 and 92 using division method..
solution
LCM( 60, 84, 92 ) = 9660
explanation
Step 1 : Write the given numbers in a horizontal line.
| 60 | 84 | 92 |
Step 2 : Divide the given numbers by smallest prime number. In this example we can divide by 2.
(if any number is not divisible by 2, write it down unchanged)
| 2 | 60 | 84 | 92 |
| 30 | 42 | 46 |
Step 3 : Continue dividing by prime numbers till we get 1 in all columns.
| 2 | 60 | 84 | 92 |
| 2 | 30 | 42 | 46 |
| 3 | 15 | 21 | 23 |
| 5 | 5 | 7 | 23 |
| 7 | 1 | 7 | 23 |
| 23 | 1 | 1 | 23 |
| 1 | 1 | 1 |
Step 4 : Multiply numbers in first column to get LCM.
LCM( 60, 84, 92 ) = 2 · 2 · 3 · 5 · 7 · 23 = 9660 .
This solution can be visualized using a Venn diagram.
The LCM is equal to the product of all the numbers on the diagram.
What is Least Common Multiple?
The least common multiple (LCM) is the smallest number that can be divided by all the given numbers. For example, LCM(8,6)=24, because 24 is divisible by 8 and 6, and it is the smallest such number.
How to calculate LCM
There are five common methods for calculating LCM. We'll use simple examples to show how to use each of these methods.
Find LCM by listing multiples
Example: find LCM of 8 and 6 by listing multiples.
Step 1: The first few multiples of 6 and 8 are:
Multiples of 6: 6, 12, 18, 24, 30
Multiples of 8: 8, 16, 24, 32, 40
Step 2: LCM is the smallest numbers that appears in both lists:
LCM (6, 8) = 24
Note:This method is unsuitable for numbers that are greater than 20.
Find LCM using prime factors
Example: Find the LCM of 8, 12 and 30.
Step 1: Prime factorizations of given numbers are:
8 = 2 · 2 · 2
12 = 2 · 2 · 3
30 = 2 · 3 · 5
Step 2: Match primes vertically
| 8 | = | 2 | · | 2 | · | 2 | ||||
| 12 | = | 2 | · | 2 | · | 3 | ||||
| 30 | = | 2 | · | 3 | · | 5 |
Step 3: Bring down numbers in each column and multiply to get LCM:
| 8 | = | 2 | · | 2 | · | 2 | ||||||
| 12 | = | 2 | · | 2 | · | 3 | ||||||
| 30 | = | 2 | · | 3 | · | 5 | ||||||
| LCM | = | 2 | · | 2 | · | 2 | · | 3 | · | 5 | = | 120 |
This solution can be visualized using a Venn diagram.
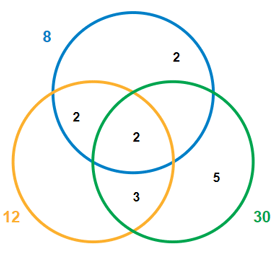
Find LCM using the ladder method
Example: Find the LCM of 84 and 112, using Ladder method.
Step 1: Place the numbers inside the division bar:
| 84 | 112 |
Step 2: Divide both numbers by 2:
| 2 | 84 | 112 |
| 42 | 56 |
Step 3: Repeat Step 2 until you can no longer divide
| 2 | 84 | 112 |
| 2 | 42 | 56 |
| 7 | 21 | 28 |
| 3 | 4 |
Step 4:LCM is a product of numbers into L shape.
| 2 | 84 | 112 |
| 2 | 42 | 56 |
| 7 | 21 | 28 |
| 3 | 4 |
LCM = 2 · 2 · 7 · 3 · 4 = 336
Find LCM using division method
Example: find LCM of 18, 24 and 60 using the division method.
Step 1: Write the given numbers on a horizontal line.
| 18 | 24 | 60 |
Step 2: Divide numbers by the smallest prime number. If any number is not divisible by 2 write it down unchanged.
| 18 | 24 | 60 | |
| 2 | 9 | 12 | 30 |
| 2 | 9 | 6 | 15 |
| 2 | 9 | 3 | 15 |
Step 3:Continue dividing by prime numbers 3, 5, 7... Stop when the last row contains only ones.
| 18 | 24 | 60 | |
| 2 | 9 | 12 | 30 |
| 2 | 9 | 6 | 15 |
| 2 | 9 | 3 | 15 |
| 3 | 3 | 1 | 5 |
| 3 | 1 | 1 | 5 |
| 5 | 1 | 1 | 1 |
Step 4:Multiply the numbers in the first column to get LCM
LCM(18, 24, 60) = 2 · 2 · 2 · 3 · 3 · 5 = 360
LCM formula
Example: find LCM of 48 and 60?
In this section we use formula
$$ \text{LCM(a,b)} = \dfrac{ a \cdot b }{ \text{GCD(a,b)} } $$Since GCD(48, 60) = 12, we have:
$$ \text{LCM(48, 60)} = \dfrac{ 48 \cdot 60 }{ \text{GCD(48, 60)} } = \dfrac{2880}{12} = 240$$2. Prime factorisation calculator
3. Prime factorisation method - video tutorial
4. LCM of three numbers - video tutorial