- Calculators
- ::
- Analytic Geometry
- ::
- Equations of a Parallel and Perpendicular Line
Parallel and perpendicular line calculator
This calculator finds an equation for a parallel or perpendicular line passing through a given point. The calculator provides a step-by-step explanation for how to obtain the result.
Find the line that is parallel to $ y = 0 $ and passes though the point $ \left(0,~0\right) $.
solution
The equation of the line parallel to the given line that contains point $ A $ is:
$ \color{blue}{ y=0 }$ ( General form )
$ \color{blue}{ y = 0 } ~~~$ ( Slope y-intercept form )
explanation
Step 1:The slope of a given line is $ m = 0 $.
Step 2: Parallel lines have the same slope, so the slope of the unknown line ($ m_1 $) will also be $ 0 $. So the parallel line will have a slope of $ m_1 = 0 $
Step 3: Now we have a point and the slope so we can use point-slope form, which is:
$$ y - y_0 = m_1 (x - x_0) $$In this example we have: $ m_1 = 0 $ , $ x_0 = 0 $ and $ y_0 = 0 $. After substitution we have:
$$ \begin{aligned} y - y_0 =& ~ m_1 (x - x_0) \\ y - 0 =& ~ 0 ( x - 0) \\y =& ~ 0\\ \end{aligned} $$How to find line through a point parallel to a given line ?
Equation of the line that passes through the point $A(x_0, y_0)$ and is parallel to the line $y = mx + b$ is:
$$ {\color{blue}{ y - y_0 = m(x-x_0) }} $$Example:
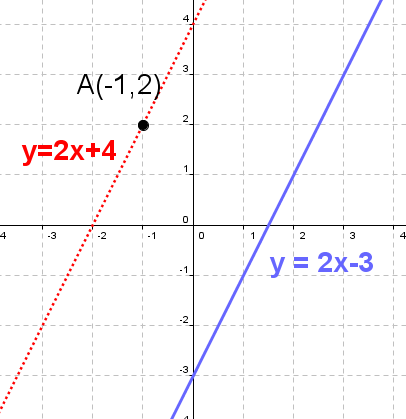
Find the equation of the line that passes through the point $A(-1, 2)$ and is parallel to the line $y = 2x - 3$
Solution:
In this example we have: $ x_0 = -1,~~ y_0 = 2,~~ m = 2$. So we have:
$$ \begin{aligned} y - y_0 & = m(x-x_0) \\ y - 2 & = 2(x-(-1)) \\ y - 2 & = 2x + 2 \\ y & = 2x + 2 + 2 \\ {\color{blue}{ y }} & {\color{blue}{ = 2x + 4}} \end{aligned} $$Note : If you want to solve this problem using above calculator, you need to rewrite line equation in general form ( $2x - y - 3 = 0$ )
How to find line through a point perpendicular to a given line ??
Equation of the line that passes through the point $A(x_0, y_0)$ and is perpendicular to the line $y = mx + b$ is:
$$ {\color{blue}{ y - y_0 = -\frac{1}{m}(x-x_0) }} $$Example:
Find the equation of the line that passes through the point $A(-1, 2)$ and is perpendicular to the line $y = 2x - 3$
Solution:
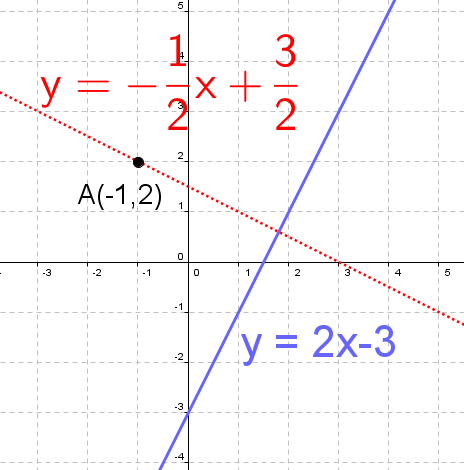
In this example we have: $ x_0 = -1,~~ y_0 = 2,~~ m = 2$. So we have:
$$ \begin{aligned} y - y_0 & = -\frac{1}{m}(x-x_0) \\ y - 2 & = -\frac{1}{2}(x-(-1)) \\ y - 2 & = -\frac{1}{2}(x + 1) \\ (y - 2)\cdot{\color{red}{2}} & = -\frac{1}{2}\cdot{\color{red}{2}}(x + 1) \\ 2(y - 2) & = -(x + 1)\\ 2y - 4 & = -x - 1\\ 2y & = -x + 3\\ {\color{blue}{ y }} & = {\color{blue}{-\frac{1}{2}x + \frac{3}{2} }} \end{aligned} $$Note : If you want to solve this problem using above calculator, you need to rewrite line equation in general form ( $2x - y - 3 = 0$ )