« Ellipse

Definitions:

1. A hyperbola is the locus of points where the difference in the distance to two fixed points (called the foci) is constant.

2. A hyperbola is the set of all points $(x, y)$ in the plane the difference of whose distances from two fixed points is some constant. The two fixed points are called the foci.

A hyperbola comprises two disconnected curves called its arms or branches which separate the foci.

Hyperbola can have a vertical or horizontal orientation.

Hyperbola centered in the origin

Standard equation of a hyperbola centered at the origin (horizontal orientation)

$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$

Example 1:

$\frac{x^2}{1} - \frac{y^2}{2} = 1$

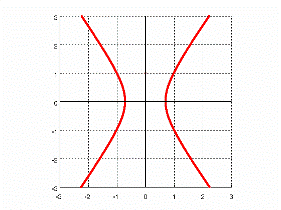
Standard equation of a hyperbola centered at the origin (vertical orientation)

$\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1$

Example 2:

$\frac{x^2}{2} - \frac{y^2}{1} = 1$

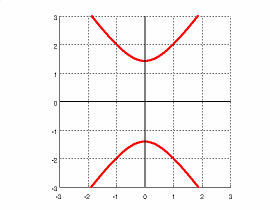
Foci

The foci for a horizontal oriented hyperbola are given by

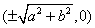
The foci for a vertical oriented hyperbola are given by

$(\pm \sqrt{a^2 + b^2}, 0)$

Asymptote:

Asymptotes of a horizontal oriented hyperbola are determined by

$y = \frac{b}{a}x$ and $y = - \frac{b}{a}x$

Asymptotes of a vertically oriented hyperbola are determined by

$y = \frac{a}{b}x$ and $y = - \frac{a}{b}x$

Eccentricity:

The eccentricity is given by

$e = \sqrt{1 + \frac{b^2}{a^2}}$

Example 3:

Consider the equation

$\frac{x^2}{16} - \frac{y^2}{9} = 1$

Find: $a$, $b$, foci, asymptotes, and eccentricity.

$$\begin{aligned} &a^2 = 16 \Rightarrow a = 4 \\ &b^2 = 9 \rightarrow b = 3 \end{aligned}$$

Foci:

$$\begin{aligned} &F1: \ \ \left( - \sqrt{a^2 + b^2}, 0 \right) = \left( - \sqrt{4^2 + 3^2}, 0 \right) = (-5, 0) \\ &F2: \ \ \left( \sqrt{a^2 + b^2}, 0 \right) = \left( \sqrt{4^2 + 3^2}, 0 \right) = (5, 0) \\ \end{aligned}$$

Asymptotes:

$$\begin{aligned} &As1: \ \ y = \frac{b}{a} x \rightarrow y = \frac{3}{4} x \\ &As2: \ \ y = - \frac{b}{a} x \rightarrow y = - \frac{3}{4} x \end{aligned}$$

Eccentricity:

$$e = \sqrt{1 + \frac{b^2}{a^2}} = \sqrt{1 + \frac{3^2}{4^2}} = \frac{5}{4}$$

Picture:

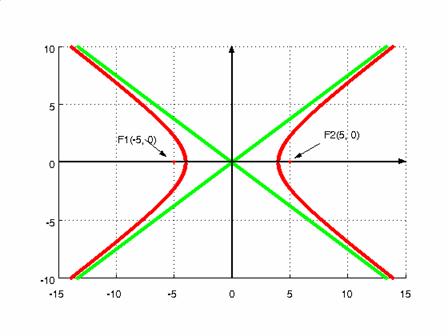
Hyperbola centered in (u,v):

Horizontal oriented hyperbola centered at $(u, v)$

$$\frac{(x - u)^2}{a^2} - \frac{(y - \nu)^2}{b^2} = 1$$

Vertical oriented hyperbola centered at $(u, v)$

$$\frac{(y - u)^2}{a^2} - \frac{(x - \nu)^2}{b^2} = 1$$

Foci:

The foci for a horizontal oriented hyperbola centered at $(u, v)$:

$$(u \pm \sqrt{a^2 + b^2}, \nu)$$

The foci for a vertical oriented hyperbola centered at $(u, v)$:

$$(u, \nu \pm \sqrt{a^2 + b^2})$$

Asymptote:

Asymptotes of a horizontal oriented hyperbola are determined by

$y = \nu + \frac{b}{a} (x - u)$ and $y = \nu - \frac{b}{a} (x - u)$

Asymptotes of a vertically oriented hyperbola are determined by

$y = u + \frac{b}{a} (x - \nu)$ and $y = u - \frac{b}{a} (x - \nu)$

Eccentricity:

The eccentricity is given by

$e = \sqrt{1 + \frac{b^2}{a^2}}$

Parametric Equations:

Horizontal oriented hyperbola:

$$\begin{aligned} &x = a \sec t + u \\ &y = b \tan t + \nu \\ &0 \le t < 3 \pi \end{aligned}$$

Vertical oriented hyperbola:

$$\begin{aligned} &x = a \tan t + u \\ &y = b \sec t + \nu \\ &0 \le t < 2 \pi \end{aligned}$$